Can Standard Deviation Be Zero
Variance and Standard Deviation
If there are no extreme or outlying values of a variable, the hateful is the most appropriate summary of a typical value, and to summarize variability in the data we specifically gauge the variability in the sample around the sample mean. If all of the observed values in a sample are shut to the sample hateful, the standard difference will exist small (i.east., close to zippo), and if the observed values vary widely around the sample hateful, the standard deviation will exist large. If all of the values in the sample are identical, the sample standard divergence will be zero.
When discussing the sample mean, we found that the sample mean for diastolic blood pressure level was 71.3. The tabular array below shows each of the observed values along with its corresponding deviation from the sample hateful.

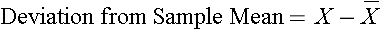
Table 11 - Diastolic Blood Pressures and Deviation from the Sample Mean
| X=Diastolic Blood Pressure | Deviation from the Hateful |
|---|---|
| 76 | 4.7 |
| 64 | -7.3 |
| 62 | -ix.three |
| 81 | 9.7 |
| 70 | -one.iii |
| 72 | 0.7 |
| 81 | 9.7 |
| 63 | -8.iii |
| 67 | -4.iii |
| 77 | 5.7 |
| | |
The deviations from the mean reverberate how far each private's diastolic blood pressure level is from the hateful diastolic blood pressure level. The first participant'southward diastolic blood pressure is iv.vii units above the mean while the second participant'due south diastolic blood pressure is 7.iii units below the hateful. What we demand is a summary of these deviations from the mean, in particular a measure of how far, on average, each participant is from the mean diastolic claret pressure. If we compute the mean of the deviations by summing the deviations and dividing by the sample size we run into a problem. The sum of the deviations from the mean is nix. This volition always be the instance equally information technology is a property of the sample mean, i.e., the sum of the deviations below the mean will always equal the sum of the deviations to a higher place the mean. However, the goal is to capture the magnitude of these deviations in a summary mensurate. To address this problem of the deviations summing to cypher, we could take absolute values or square each divergence from the mean. Both methods would address the problem. The more pop method to summarize the deviations from the mean involves squaring the deviations (absolute values are difficult in mathematical proofs). Tabular array 12 beneath displays each of the observed values, the corresponding deviations from the sample mean and the squared deviations from the mean.
Table 12
| X=Diastolic Blood Pressure level | Departure from the Mean | Squared Deviation from the Hateful |
| 76 | four.7 | 22.09 |
| 64 | -7.3 | 53.29 |
| 62 | -9.three | 86.49 |
| 81 | 9.7 | 94.09 |
| seventy | -ane.iii | 1.69 |
| 72 | 0.7 | 0.49 |
| 81 | nine.7 | 94.09 |
| 63 | -8.3 | 68.89 |
| 67 | -4.iii | 18.49 |
| 77 | 5.7 | 32.49 |
| | | |
The squared deviations are interpreted as follows. The first participant's squared deviation is 22.09 significant that his/her diastolic blood pressure is 22.09 units squared from the mean diastolic claret pressure, and the second participant'south diastolic blood force per unit area is 53.29 units squared from the mean diastolic blood pressure. A quantity that is oftentimes used to measure variability in a sample is called the sample variance, and information technology is essentially the mean of the squared deviations. The sample variance is denoted s2 and is computed every bit follows:

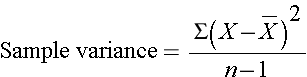

 | Click beneath the question to view the answer. |
| This content requires JavaScript enabled. | |
In this sample of n=10 diastolic blood pressures, the sample variance is s2 = 472.x/ix = 52.46. Thus, on average diastolic claret pressures are 52.46 units squared from the mean diastolic blood pressure. Because of the squaring, the variance is not especially interpretable. The more than mutual measure out of variability in a sample is the sample standard deviation, defined as the square root of the sample variance:

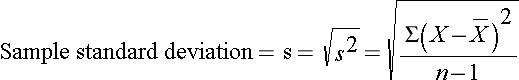
Can Standard Deviation Be Zero,
Source: https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_summarizingdata/bs704_summarizingdata6.html#:~:text=If%20all%20of%20the%20values,standard%20deviation%20will%20be%20zero.
Posted by: hillpoetastords1990.blogspot.com

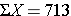
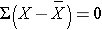
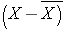
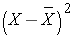
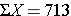
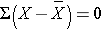
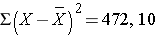

0 Response to "Can Standard Deviation Be Zero"
Post a Comment